扇形计算法，可用于判断攻击方向，前方是否有玩家等等

[冷颜的午睡日常]

下方是源代码，带有注释：

function GetVector3Dot(v1, v2) --计算向量
    return v1.X * v2.X + v1.Y * v2.Y + v1.Z * v2.Z
end
function aradius(ros1,ros2,pos1,pos2,r,angle)
--r是扇形半径，angle是角度，要表示在前方，角度为180度就行了
--ros1是物体1的朝向（Orientation），ros2是物体2的朝向（Orientation），pos1是物体1坐标，pos2是物体2坐标
    local t0 = ros1.Y
    local t = t0*math.pi/180 --玩家当前朝向于z轴正向夹角
    local v1 = Vector3.new(math.sin(t),0,math.cos(t))*(-1) --玩家本身单位向量
    local pos = pos2 - pos1
    local poss = pos/(pos.X*pos.X+pos.Y*pos.Y+pos.Z*pos.Z)
    local possuc = Vector3.new(poss.X,0,poss.Z)
    local cos = GetVector3Dot(v1, possuc)/(angle*angle)
    local j = math.acos(cos)
    local jd = j*180/math.pi
    if jd < angle/2 then
         return true
    --在范围内返回true
    else
         return false
    end
end
--后面判断true或者false，如果是true证明物体在前面

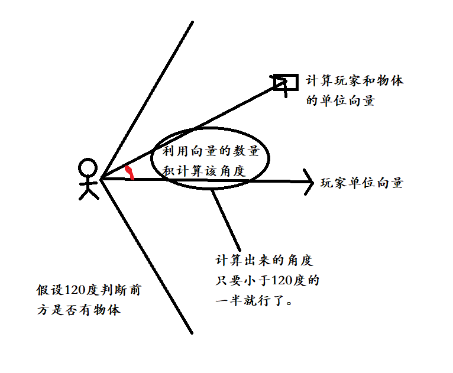
逻辑计算大概就是，以part1为原点，给一个范围角度，计算part1向前的方向向量（单位向量），然后计算part1和part2的方向向量，高中学过，有两个点的坐标就可以计算出向量坐标，从而计算出单位向量，然后使用数量积，可以计算出part1向前单位向量和两部件方向向量的cos值，从而计算出角度，角度小于给定角度的一半，就可判断物体在范围内了。

如果加上判断距离的，就是真正的扇形了。

建议直接按照注释拿来使用。

[萤火虫]

GetVector3Dot 直接用 Vector3:Dot(other) 就可以。
如果我不知道前面有没有物体 有没有办法可以获取到，比如直接返回我前方 给定距离 给定夹角范围内的对象列表。

[冷颜的午睡日常]

可以的，把需要检测的物体放进一个文件夹，
local part = script.Parent
local this = {}
for k,v in pairs(文件夹:GetChildren()) do
–这里写的是获取v和part的距离
if 距离<15 and aradius(ros1,ros2,pos1,pos2,r,angle) then --如果小于15距离和在夹角范围内
–将v存进this表里
end
end
–最后this表就是在范围的对象了，如果对象是分组的模型，那就得加上ClassName的判定等等。

[萤火虫]

不错~~ 回头试试

[永远滴神]

666，谢谢大佬分享

[小猪神]

谢谢 在群里收到你的回复了

[冷颜的午睡日常]

上面的代码有一些小缺陷，这是完美版的扇形检测代码

   function GetVector3Dot(v1, v2) --计算向量
       return v1.X * v2.X + v1.Y * v2.Y + v1.Z * v2.Z
   end
   function skill.aradius(ros1,ros2,pos1,pos2,r,angle)
        --r是扇形半径，angle是角度
        local t0 = ros1.Y
        local t = t0*math.pi/180 --玩家当前朝向于z轴正向夹角
        local v1 = Vector3.new(math.sin(t),0,math.cos(t))*(-1) --玩家本身单位向量
        local pos = pos2 - pos1
        local poss = pos/math.sqrt(pos.X*pos.X+pos.Y*pos.Y+pos.Z*pos.Z)
        local possuc = Vector3.new(poss.X,0,poss.Z)
        local cos = skill.GetVector3Dot(v1, possuc)
        local j = math.acos(cos)
        local jd = j*180/math.pi
        return jd < angle/2
    end

[萤火虫]

分享另一种方法，获取部件A与部件B的角度差。 正面是0度， 正侧面是90度 反面是180度。

 --玩家角色朝向(部件A所面对的方向)
local AFacing = Character.HumanoidRootPart.CFrame.LookVector
--从部件A到部件B的方向
local Vector = (PartB.Position - Character.HumanoidRootPart.Position).unit
--弧度
local Angle = math.acos(AFacing:Dot(Vector))
--输出角度差
print(math.deg(Angle))